Bell's Inequality

Alice and Bob - Entangled photons

Entangled photons, nonlocality and Bell inequalities
in the undergraduate laboratory.
Dietrich Dehlinger, M. W. Mitchell
(http://arxiv.org/PS_cache/quant-ph/pdf/0205/0205171v1.pdf)

The experiment described and performed by Dehlinger and Mitchell centers around the detection of photon pairs at two different locations. The polarization of a photon stream is first fixed in a specific direction from vertical with a linear polarizer, then the phase of one component is fixed with a birefringent quartz plate. The photon stream is then directed at beta barium borate (BBO) crystals that cause a small fraction of the laser photons to spontaneously decay into photon pairs with the same total energy as the original photon (a process called spontaneous parametric downconversion).

Two single-photon counting modules (SPCMs), are used to detect the photons. One detector is traditionally named Bob and the other Alice. Because the photons of a downconverted pair are produced at the same time they cause coincident, i.e., nearly simultaneous, firings of the SPCMs. Simultaneous firings are considered coincidences if they occur within 25 nanoseconds of each other. The experiment is done by recording the number of coincidences that occur for various settings for the measurement angle of Bob and Alices detectors. The number of coincidences at different observer angles is what must be modelled correctly as a “local realistic hidden variable theory” (HVT).

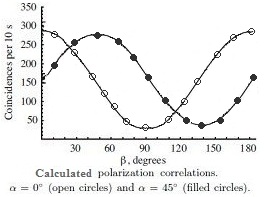
Dehlinger and Mitchell go on to obtain the results a) on the right. The open circles representing Alice at 0° and Bob at 0 to 180°. The closed circles represent Alice settings at 45° and Bob at 0 to 180°.

In the authors model, each photon has a polarization angle λ. When a photon meets a polarizer set to an angle γ , it will always register as Vγ if λ is closer to γ than to γ + π/2, i.e.,

  • if |γ − λ| ≤ π/4 then vertical
  • if |γ − λ| > 3π/4 then vertical
  • horizontal otherwise.

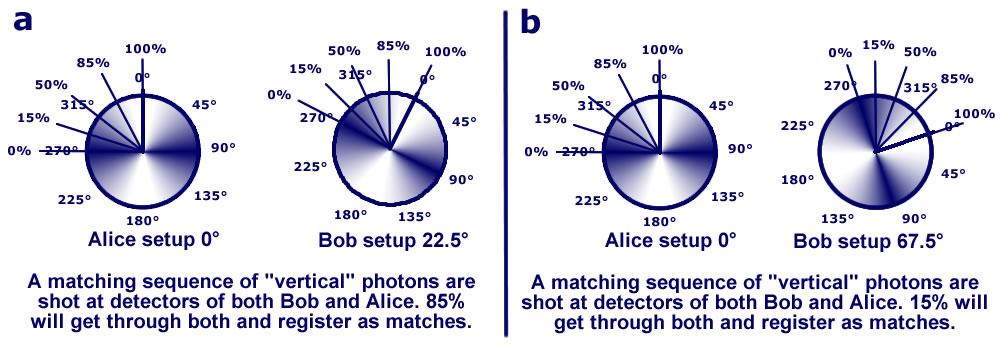
    • Represented by icons, this model produces a correlations chart, shown as b) on the right, clearly different from the experimental results shown as a). The angle 22.5° shows the most difference between the model and quantum physics. Dehlinger and Mitchell choose this angle to analyse in detail and show that their experimental results match with quantum physics. In their words "Our HVT is very simple, and yet it agrees pretty well with quantum mechanics. We might hope that some slight modification would bring it into perfect agreement.".

    Animated Physics derives the linear photons as not only having a specific "average" direction, but also as having a "wobble" or "instantaneous" direction. Represented as icons, photons present a more "fuzzy" picture of their polarization. The sample 24° photon, with a 30° wobble, will 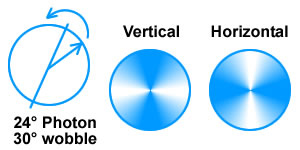most of the time be picked up as a vertical, but sometimes when the angle is over 45°, it will be picked up as a horizontal. In general, wave plates will turn both the average and the instantaneous orientation, but the path of the photon through calcite will be determined by the instantaneous orientation. The graph on the right demonstrate that this model matches the predictions of experiment. In fact, this follows (and verifies) the same cos(γ − λ)² rule that is used by quantum mechanics.

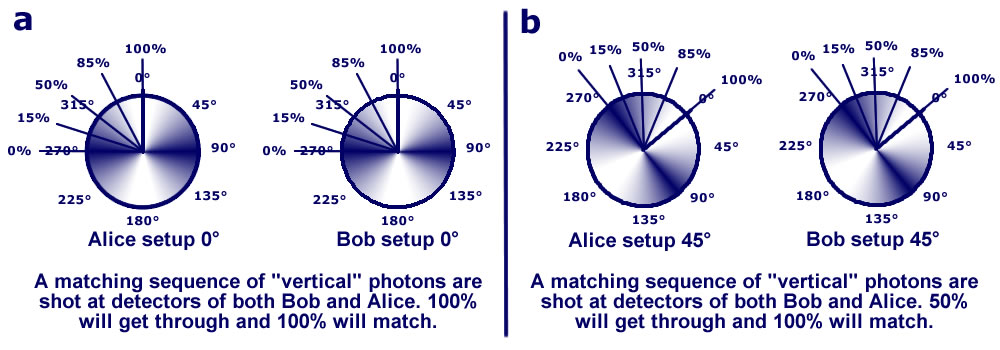
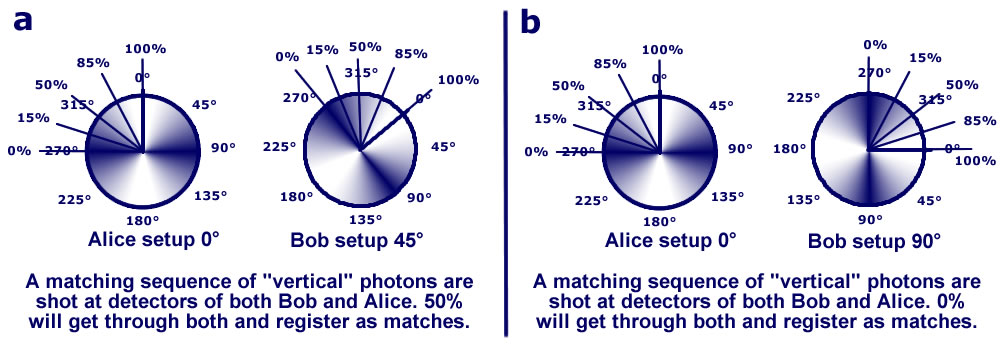
    Lets start the experiment. To start, we test that Alice and Bob get maximum matches with both set at 0°and adjust to maximize when both are at 45°.


    We leave Alice at 0° and try Bob at 45° then 90°

    Try a difference of 22.5° then 67.5° between Alice and Bob

    John Stewart Bell
    (28 June 1928 – 1 October 1990)

    "It has been argued that quantum mechanics is not locally causal and cannot be embedded in a locally causal theory. That conclusion depends on treating certain experimental parameters, typically the orientations of polarization filters, as free variables. But it might be that this apparent freedom is illusory. Perhaps experimental parameters and experimental results are both consequences, or partially so, of some common hidden mechanism. Then the apparent non-locality could be simulated."

    In 1964, after a year's leave from CERN that he spent at Stanford University, the University of Wisconsin–Madison and Brandeis University, he wrote a paper entitled "On the Einstein-Podolsky-Rosen Paradox". In this work, he showed that carrying forward EPR's analysis permits one to derive the famous Bell's theorem. The resultant inequality, derived from certain assumptions, is violated by quantum theory.

    There is some disagreement regarding what Bell's inequality—in conjunction with the EPR analysis—can be said to imply. Bell held that not only local hidden variables, but any and all local theoretical explanations must conflict with the predictions of quantum theory.

    Some people continue to believe that agreement with Bell's inequalities might be saved. They argue that in the future much more precise experiments could reveal that one of the known loopholes, for example the so-called "fair sampling loophole" or others, had been biasing the interpretations.

    Animated Physics

    A photon, created by an electron falling from one energy level to another, carries the original precession of the electrical axis of the electron and presents it as a "wobble" in the electrical axis as the photon comes directly at you. Click to see a visualization of photons derived from the axioms of animated physics.

    Although all photons travel at the speed of light, a photon's energy is related to its wavelength. High energy photons expand and contract very quickly, low energy photons expand and contract more slowly.

    Low energy photons will grow to large sizes (wavelength) compared to a higher energy photon that will only grow much smaller in size.

    Entangled photon pairs created from a single photon carry not only the polarization of their parent, but also any "wobble" the parent may have had. When we speak of photons as "entangled" we mean their polarization is related, and measuring the polarization of one, will tell us the polarization of the other.

    Here we see how the properties of photon polarization are modeled. Animations done show that they match with quantum physics (and thus with reality) and demonstrate how Bell's inequality relates within this model. Specifically, we show how an individual photon with an average vertical polarization, has a very real chance of being measured as a horizontal photon if only its instantaneous direction is taken into account.

    Experimental results

     Relative  Angle % Measured
    Vertical   Horizontal
    0°100%0%
    22.5°85%15%
    45°50%50%
    67.5°15%85%
    90°0%100%
    112.5°15%85%
    135°50%50%
    157.5°85%15%
    180°100%0%
    and specifically:
    30°75%25%
    60°25%75%

    © Animated Physics