The 61 Elementary Particles of Animated Physics
|
Types |
Generations |
Antiparticle |
Colors |
Total |
| Higgs |
1 | 1 | Own | None | 1 |  |
| W |
1 | 1 | Pair | None | 2 | 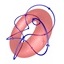 |
| Z |
1 | 1 | Own | None | 1 | 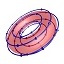 |
| Photon |
1 | 1 | Own | None | 1 |  |
| Leptons |
Charged
Neutral | Electron Muon Tau
Neutrino Neutrino Neutrino | Pair | None | 12 | 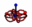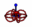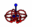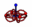 |
| Quarks |
Positive
Negative | Up Charm Top
Down Strange Bottom | Pair | 3* | 36 | 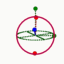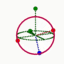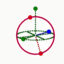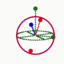 |
| Gluons |
1 | 1 | Own | 8* | 8 |  |
| Total | 61 |
* Quark color refers to the 3 possible positions in the baryon.
* Gluon color refers to the 8 possible combinations of properties (1/ in or out, 2/ up or down, 3/ left or right) the gluon can have. |
Hermann von Helmholtz (August 31, 1821 – September 8, 1894) was a German physician and physicist who
studied fluid dynamics. Specifically, Helmholtz studied vortexes in fluids and developed three theorems which still stand today.
The second of Helmholtz's theorems for vortex dynamics in inviscid fluids:
- A vortex filament cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path.
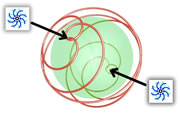
 | | 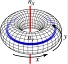 | 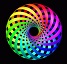 |  | 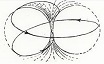 |
| Sample Vortex | | Closed Loop Vortexes |
In addition to his theorem's in fluid dynamics, in the area of vector calculus, Helmholtz's
fundamental theorem of vector calculus states that any sufficiently smooth, rapidly decaying vector field
in three dimensions can be resolved into the sum of an irrotational (curl-free, longitudinal component) vector field and a
solenoidal (divergence-free, transverse component) vector field; this is known as the Helmholtz decomposition.
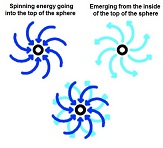
| The particles of Animated Physics come from swirling energy vortexes built from the most
basic vortex of swirling energy, the Higgs Boson. The Higgs has only transverse components of spin and is unstable with a lifetime around 1.6×10‾²² seconds. |
Higgs Boson
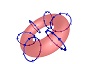 |
Mass: ~125 GeV
Charge: 0
Spin: 0 |
The Higgs boson is its own anti-particle, capable of destroying itself.
|
|
| A Higgs boson weighing 125 GeV has a 23.3% chance of decaying into a W+/W- particle combination
and a 2.9% chance of decaying into a pair of Z bosons. Both W and Z bosons have longitudinal components of spin
and are unstable with a lifetime around 3 x 10‾²⁵ seconds. |
W+ Boson
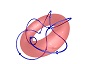 |
Mass: ~80 GeV
Charge: +1
Spin: 1 |
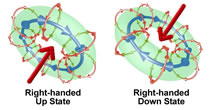
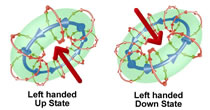
The W+ and W- bosons are anti-particles to each other. If you follow the longitudinal spin with your fingers, your
thumb must point up making the W+ a right-handed particle.
|
W- Boson
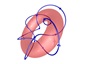 |
Mass: ~80 GeV
Charge: -1
Spin: 1 |
If you follow the longitudinal spin with your fingers, your
thumb must point down making the W- a left-handed particle.
|
Z Boson
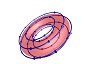 |
Mass: ~91 GeV
Charge: 0
Spin: 1 |
The Z boson is its own anti-particle and has longitudinal spin with no transverse component of spin.
|
| The W and Z bosons, being spin 1 particles, change the direction of spin
of other particles they hit. A spin up electron (+1/2) will become a down electron (-1/2). The W bosons
having a +1 or -1 charge, will change the charge of particles they hit. A +1/3 charge quark
will be changed to a -2/3 charged quark if hit by a W- boson. |
 |
The Electron and other Leptons
|
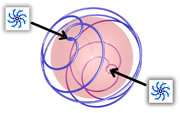
The electron looks much like a Higgs Boson trapped around a Z boson, but acts very different to both.
An electron contains a tiny mass, a strong electrical charge,
and a large (relative to other particles) magnetic moment. The electron was derived by
Paul Dirac as two coupled
2-spinors where the mass is equal to the coupling constant of the interaction.
In an electron, a strong electrical current has trapped an orthogonal magnetic field.
One spin around the electrical loop is only 1/2 a spin around the magnetic field.
A double spin of 720° is required to return the electron to its original orientation.
| Electrons | | Anti-Electrons |
Mass: 0.51 MeV
Charge: -1
Spin: 1/2
Magnetic: −1.0 μʙ |
 |
|  |
The electron is a lepton and is very stable. The electron has two heavier unstable cousins with the same charge, spin, and only tiny differences in their magnetic moment.
The Muon has a mass of 106 MeV and the a Tau has a mass of 1,777 MeV.
 |
Quarks, Mesons and Baryons |
Up Quark +2/3 charge
 |
Down Quark -1/3 charge
 |
Making a Gluon
 |
A Higgs boson weighing 125 GeV has a 56.1% chance of decaying into a Botton/Anti-Bottom quark particle combo.
Quarks are large empty 3D spinning spherical shells with both longitudinal and transverse components of spin.
Quarks colored blue symbolize a +2/3 charge and red symbolizes a -1/3 charge.
When layered, these spheres make up Mesons and Baryons. Mesons have two layers of quark shells, Baryons have three layers.
Protons and Neutrons (both three layered Baryons) are the final, and most noticeable, decay products.
Quark shells are able to stack or layer together with the help of gluons. Gluons act both as "lubercant" between quark layers and
as special "taps" that allow energy to flow in or out of a particular region.
8 Gluon Styles
 | |
An important attribute of spin on a quark is what happens at the poles. If you follow the spin of an individual
point on the surface of the shell, you will notice it goes directly through both the north and the south pole of the quark on every turn.
This means a lot of paths are directly converging and diverging at the poles. To accommodate this we assume the converging
lines are coming in either above or below the outgoing diverging lines. Also, the left or right handedness of the poles
tells us which way the magnetic field is pointing for both regular and anti-quarks.
The properties of the gluon is called its color charge. There are three color charges, specifically spin (clockwise or counterclock)
magnetic direction (up or down) and flow (in or out), making 8 unique gluons.
The "Color charge" rules are detailed in
quantum chromodynamics (QCD), and are a basis for the interaction of quarks and gluons
to form more complex elements.
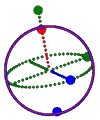 | The Proton Quarks: udu
Mass: 938.272
Charge: +1
Spin: 1/2
|
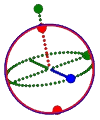 | The Neutron Quarks: udd
Mass: 939.565
Charge: 0
Spin: 1/2
|
 |
The Wave Nature of Particles, Photons and Neutrinos
|
To discuss the last two styles of particles, we need to introduce the idea of the wave nature of particles
and wave equations with respect to these particles. A wave equation describes the periodic or constantly changing properties of a particle
as it travels through time and/or space. Photon and neutrino properties cannot be discussed without
the framework of a wave equation.
 |
All particles can exhibit wave properties.
A particle that expands and contracts as it moves, will behave
differently if it hits another particle when expanded compared to when it is contracted.
In 1924, a physicist named Louis deBroglie proposed that the electron would exhibit a wave-like nature based on
the electrons kinetic energy. His theory, together with the Davisson-Germer experiment done in 1927, established
that an electron, accelerated by an electric field does have wave properties. Based on deBroglie's calculations, an electron, accelerated through
a field of 54 volts, has a wavelength of 0.167 nanometers. Based on this wavelength, the electron takes
5.6 attoseconds to complete one expansion/contraction cycle. When these electrons are shot at a surface of
nickel atoms where the spacing between atoms is a similar size, the electrons show a recoil pattern that
allowed the spacing between the nickel atoms to be calculated.
The wave nature of electrons is only visible when the electrons are accelerated to very high speeds. For photons, the wave
properties have significant impact, allowing for the understanding of refraction, defraction and interference
in groups of photons. For neutrinos, the wave nature is even more important as the neutrino type also changes in a periodic
manner. Additional detail and graphics on photons and neutrinos will be coming soon in the next article.
In Summary
The physicist Eugene Wigner, in 1960, published a famous essay,
The Unreasonable Effectiveness of Mathematics in the Natural Sciences.
In it he shows that abstract mathematical concepts hold validity far beyond those for
which they were developed. Riemann's 19th century studies in non-Euclidean geometry form the basis of
Einstein's thinking on gravitation and the codification of the rotational groups of abstract solids
led to the successful prediction of the Higgs Boson. Mathematics has led
us to a much better predictive capability of how the world around us works, but leaves a barren landscape in our
ability to understand and make sense of it all. Computer animations and simulations are able
to bridge that gap and bring sense to this complex mathematical description.



