Ground state of the Hydrogen Atom
By Ed UnverrichtJanuary 1, 2010
Learn About
Stable Electron Orbits
Electron Clouds
van der Waals Force
Hydrogen Molecules
Abstract:
In this paper we use a fixed grid and fixed timesteps, similar to frames in a movie, to model the Hydrogen molecule. Two objects, the electron and the proton, are defined with their traditional charge and coulomb forces with one exception. The electron and proton exert no force on each other if they are within a Bohr radius (53 picometers) of each other. This exception allows us to accurately model the Hydrogen molecule such that there are no known conflicts with its properties in the real world.
Important properties are demonstrated using animations controlled by these forces. Stable orbits of electrons and protons are shown up to the ionization energy of 13.6 evolts for Hydrogen using attosecond timeframes. Electron clouds and a picture of uncertainty arise at the femtosecond timeframe. The van der Waals Force that draws even zero charge molecules together and the stable forms of hydrogen chemical bonds are simulated.
|
With the electron not feeling any force from the proton inside a 53 picometer radius, the electron becomes effectively "stuck" or "bonded" to the proton. If some force takes it outside the 53 picometer radius of the proton, it will be drawn back in due to the normal electromagnetic force from the proton. This same property allows the electrons to act as "glue" to hold two protons together in a covalent bond.
Finally, since the electron does not feel any acceleration within the proton, it also does not generate significant radiation and begin an endless spiral into the center of the proton.
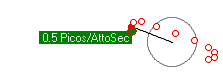
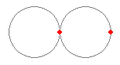
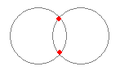
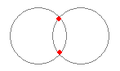
Stable orbits were generated for a wide variety of low energy orbits. Figures 1 (a) and (b) show how an electron remains bound to a proton with energies as low as 1.2evolts to as high as 9.0evolts. Figure 1 (c) shows how two electrons form two independent orbitals around the proton and can remain stable with electron energies over 2.0evolts. All proton/electron forces are calculated using Coulomb's inverse square law for values of r greater then 53pm, and set to 0 for any value of r less than 53pm. All electron/electron forces are calculated using Coulomb's inverse square law no matter the separation distance.
Coulomb's Law: if r>53 F = ke(qeqp/r2)
Quantum effect: if r<53 F = 0
- qe is the charge force of the electron (-1.6×10−19 coulombs)
- qp is the charge force of the proton (1.6×10−19 coulombs)
- ke = 8.99 Nm2/c2
The position, velocity and acceleration of all electrons and protons are calculated subject to Newtons laws using one attosecond time steps and displayed using 10 attosecond intervals. Ten frames are shown for a total elapsed time of 100 attoseconds. Little motion of the proton is detectable at these timescales given its much larger mass.
- me is the mass of the electron (9.1×10−31 kilograms)
- mp is the mass of the proton (1.67 x 10−27 kilograms)
Fixed Position Electron Clouds
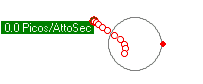
The electron orbits above, produce very different patterns when viewed at a much slower timescale. Figure 2 shows the same orbits and uses the same calculations as Figure 1. Figure 2 displays the location of the electron every 200 attoseconds over 30 frames for a total elapsed time of 6000 attoseconds (6 femtoseconds). Both Figures 1 and 2 calculate the position of the electrons and protons using one attosecond time steps. The filled red dots are the starting location of the electrons.
Figure 2.
Electron Clouds 53pm radius Frame rate = 200 AttoSeconds/frame 30 frames shown |
(a) PE+KE = 9.0ev 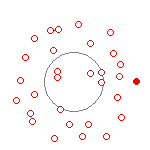 |
(b) PE+KE = 1.2ev  |
(c) PE+KE = 2.0ev 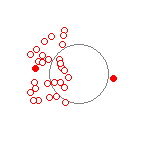 |
Figure 2 (a) and (b) show what a hydrogen atom would look like when probed at a timescale of every 200 attoseconds. It is impossible to track the orbit of the electron at this timescale. All you see is a collection of what looks to be random points inside a somewhat bounded area. It is clear the more energy the electron has, the more diffuse the pattern becomes. An electron of 9 evolts (a) produces a diffuse cloud of almost 150 picometer radius (1.5 angstroms). Lower energy hydrogen atoms (b) produce a more tight diffusion pattern, but we dont see the electron cloud ever go to less then 53 picometers radius at this time scale unless the electron has very close to zero energy.
Figure 2 (c) shows what one of the electron clouds would look like when probed every 200 attoseconds over a 6 femtosecond time interval. The picture displays the motion of only one of the electrons of a two electron, one proton system. The other electron is also moving but its motion is not shown for simplicity.
Hydrogen van der Waals forces are small forces that attract molecules together even though some have a neutral charge. Table 1 displays calculated van der Waals forces that attract a proton to a neutral hydrogen molecule for different proton/proton separation distances. The force is due to the electron being closer to the proton than the other proton. Distances are given in Angstroms and force in NanoNewtons. This force is very small but attractive at large distances, slowly grows larger as the objects get closer and finally becomes negative as the objects get very close.
Table 1
|
Proton/Proton Distance in angstroms |
Electron |
Proton Force |
Electron |
Total Force |
|
4 |
3.5 |
-1.4 |
1.9 |
0.5 |
|
3 |
2.5 |
-2.6 |
3.8 |
0.8 |
|
2 |
1.5 |
-5.8 |
10.7 |
4.9 |
|
1 |
0.5 |
-23.1 |
0 |
-23.1 |
More complex systems of electrons and protons were studied to determine the properties of Hydrogen molecules that form under these quantum conditions. From time to time, the momentum of the particles is cleared to allow the electrons to "fall" into their lower energy levels. Clearing particle momentum has the effect of stabilizing the structure of electrons and protons for brief periods of time. If the structure is fundamentally unstable, it will fall apart after the momentum is cleared due to normal forces associated with the particles. A number of stuctures do not fall apart and remain stable over very long periods of time. The properties of these structures can be determined by simulations and provide a method to experimentally prove or disprove the values of the quantum forces chosen.
|
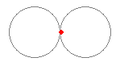
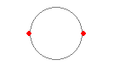
Figure 3. Stable forms of Hydrogen 53pm radius |
(a) H2+ cation (base) |
(b) H- anion (acid) |
(c) Para Hydrogen |
(d) Ortho Hydrogen |
The only stable structure found for two protons and one electron is shown in Figure 3 (a). The electron gets caught in the 53 picometer shell of one of the hydrogen protons (called proton1) and sits on the side closest to the other hydrogen proton (called proton2). Proton2 is drawn to proton1 as the force from the electron is stronger than the force from proton1 due to the location of the electron (it is 53 picometers closer). Once proton2 is within 106 picometers of proton1 it is no longer attracted to the electron as the electron is now within 53 picometers of proton2. This structure sticks together since the repulsion of the protons is not strong enough to pull the electron out of either of the proton shells. This structure is long lived and stable both experimentally and in theory.
The only stable structure for two electrons and one proton is displayed in Figure 3 (b). Both electrons are pushed away from each other as much as they can. If they separate any more than 106 picometers, one or the other is pushed outside the proton shell and it feels the normal coulomb force pulling it back in.
There are two stable structures for two protons and two electrons as displayed in Figures 3 (c) and (d). Both structures form naturally in the sense that the coulomb and quantum forces draw the particles together. Clearing momentum from time to time keeps the structure from immediately drifting apart and results in stable bonds of both types. Both para and ortho hydrogen are found in large quantities throughout the universe.
Full animations available at http://www.animatedphysics.com