Exploring the Sun
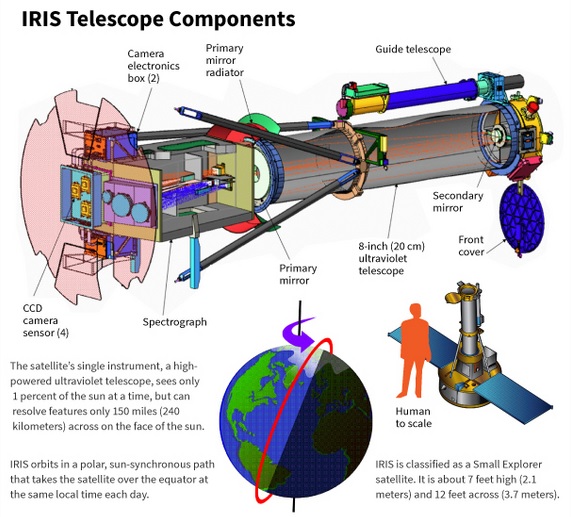
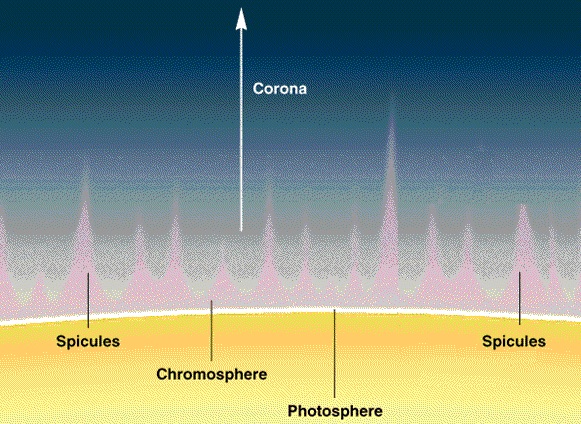
A spacecraft called IRIS (Interface Region Imaging Spectrograph) studies the suns atmosphere. Material that travels through the atmosphere, known as the solar chromosphere, heats up from about 10,000 degrees Fahrenheit (5,500 degrees Celsius) at the sun's surface to temperatures as high as 3.5 million degrees Fahrenheit (2 million degrees celsius) farther out.
The ultraviolet telescope studies "how solar material moves, gathers energy and heats up" in the chromosphere on its way to the outer atmosphere, the corona. The Sun is almost perfectly spherical and exists as a large ball of hydrogen. The hydrogen has become so compressed by gravitational forces that 620 million metric tons of hydrogen fuse into helium each second. The task of IRIS is not to study the interior, but to make sense of the layers of hydrogen on the outer edge of the sun.
Modelling the Hydrogen Atom
The ionization energy needed to remove an electron from a neutral hydrogen atom is 13.6 eVolts. The Bohr radius of hydrogen has a value of 52.9 picometers (10^-11 meters). The force holding a single electron to a single proton never grows higher then the value calculated with coulombs law at this distance. This value can be also computed in terms of other physical constants including the permittivity of free space, the speed of light in vacuum and other constants found in nature. At this distance, it takes 13.6 eVolts of energy to knock this electron away from the proton and it never takes more then 13.6 eVolts of energy to ionize hydrogen no matter how close the electron is to the proton.
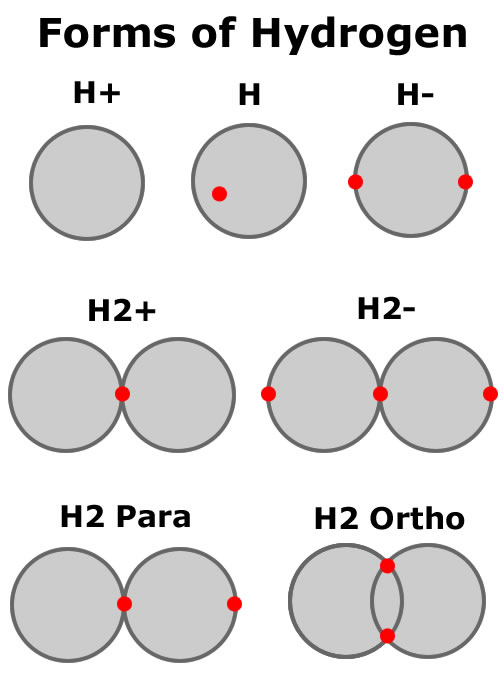 |
Electrons and protons are attracted inversely proportional to the squared distance between them if the electron is outside the proton shell of 53pm. Electrons feel no force from the proton while inside the proton shell. Bonding between hydrogen protons happens as one electron, trapped in a proton of one hydrogen, gets trapped in a proton of another hydrogen, binding the two hydrogens together.
A proton and an electron combination (hydrogen) is neutral in charge. Although neutral, the proton acting as a shell of charge with the electron close to the edge of the shell, will attract other neutral hydrogen atoms until one electron (or perhaps 2 in the ortho form) is trapped in both hydrogen shells binding them together.
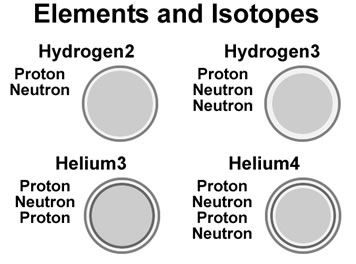 The neutron is a shell in the same manner as the proton, but without the electric charge (white shell in figure). Protons and neutrons are
allowed to flow through each other, but when the shells are very close, they feel the effect of the strong
force. The strong force is a binding force that merges shells together if they are forced to be very close to each other.
A proton and neutron shell is less then one femtometer thick while its size is thousands of times larger at over 52 picometers.
Elements are modelled as proton and neutron shells, stacked on each other, binding together,
with the neutrons acting as an insulators between proton shells. On heavier elements, extra neutron shells between some
of the layers provide a more stable element.
The neutron is a shell in the same manner as the proton, but without the electric charge (white shell in figure). Protons and neutrons are
allowed to flow through each other, but when the shells are very close, they feel the effect of the strong
force. The strong force is a binding force that merges shells together if they are forced to be very close to each other.
A proton and neutron shell is less then one femtometer thick while its size is thousands of times larger at over 52 picometers.
Elements are modelled as proton and neutron shells, stacked on each other, binding together,
with the neutrons acting as an insulators between proton shells. On heavier elements, extra neutron shells between some
of the layers provide a more stable element.
Hydrogen Energy Levels
Left alone, an electron falling into a proton, may get trapped or "bonded" to a shell. The amount of energy that is released when an electrion "binds" to the proton shell, spends on the local vibrations of the proton shell. Click the video on the right to see the vibration modes of the proton. The first 4 seconds are S levels, then P levels and more complex vibrational patterns. If a free electron initially gets trapped on the P2 energy level, it will emit a photon of 3.4 eVolts. Over time, the vibrations subside and the vibration pattern transitions from P2 to S1 where a 10.2 eVolt photon will be emitted and the electron ends up in the stable lowest energy level and is bound to the proton shell with a total of 13.6 eVolts.
To model photon emissions, the energy of the photon emitted is determined by the energy level that the electron came from subtracted from the energy level of where the electron ends up.
The energy level the electron is in, depends on the vibration pattern of the proton shell it is bonded to. In a low density environment, most of the protons in a hydrogen gas will stablize their vibration pattern and the electron will fall to the lowest energy level. In a higher density electron gas, the proton shells are much less stable and electrons jump around from one higher energy level to another high energy level due to the variance of the proton shell vibration pattern. In fact, if packed tight enough, the proton shells start to overlap and the electrons become more energenic and less stable on a particular level. Electrons are more likely to emit photons due to a jump from higher energy levels like 8 or 9 when protons are more closely packed together.
Modelling the heat of hydrogen
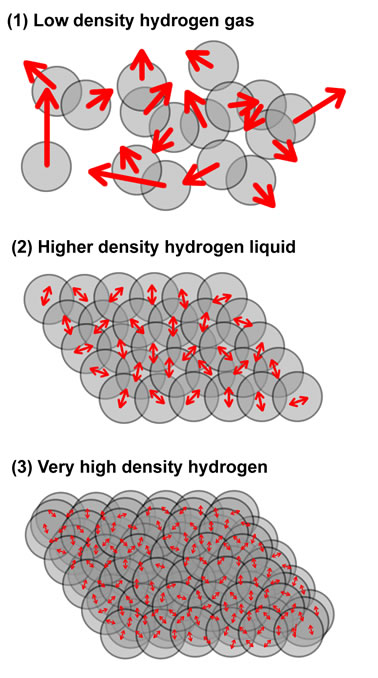
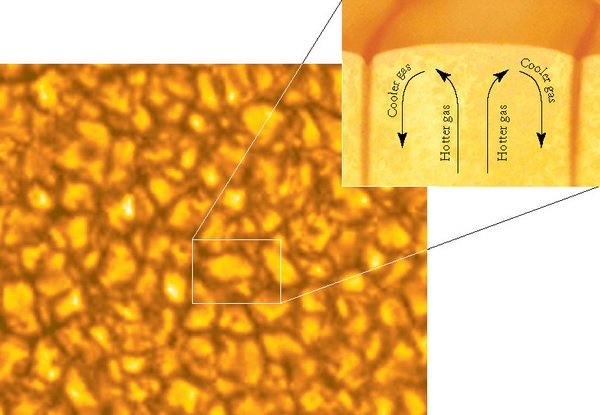
Measuring the temperature of a hydrogen gas or liquid is fundamentally a measure of the movement of the hydrogen proton. The electrons contributes to bonding and emissions, but since it has such a small mass compared to the proton (some 1000 times smaller), the movement of the electon does not contribute in a significant way to the heat.
Low density hydrogen gas can attain extremely high temperatures, due to the freedom of motion of the molecules. The speed that the hydrogen molecule can attain is only limited by the speed of light and the number of collisions with other hydrogen molecules.
As hydrogen gas is compressed the freedom of motion is significantly impaired. At very high pressures, the hydrogen gas forms a liquid and the motion of the protons undergoes a phase transition. The motion evolves from being relatively independent of other molecules except for the case of collisions, into an ordered state where a molecule no longer flies around randomly but now is so constrained by the other molecules and is only able to "vibrate in place". As in any other material, the temperature that a gas can obtain, greatly exceeds the temperature a liquid or solid of that same material can reach due to the constraint in motion of the individual molecules.
The Sun
The sun is a very large ball of mostly hydrogen held together by its own gravitational force. This force grows so large, that towards the center of the sun, hydrogen molecules are so compressed that the stong nuclear force takes over and hydrogen is converted to helium.
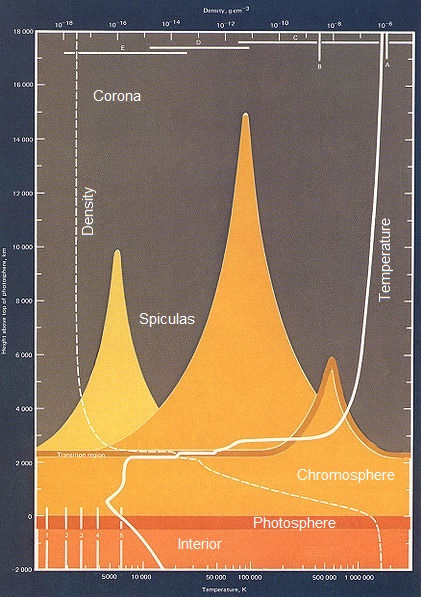 |
As you descend through the chromosphere the density rises up to 5×10^−6 kg/m³. The temperature drops as the mobility of the hydrogen proton begins to be restricted by other protons in the neighborhood. With significant overlap of the protons, we see a lot higher energy level transitions.
The phase transition from hydrogen gas to the hydrogen liquid on the surface of the sun (called the photosphere) occurs at 5,778 K°, where the density is 2×10^−4 kg/m³. Hydrogen protons cannot "fly around" anymore and hydrogen flows like any other liquid.
 Falling deeper into the sun, the density rises eventually to 1.6×10^5 kg/m³. The movement of protons and electrons
are so severely restricted that electrons bind with protons forming neutrons. This process is a reverse
beta-decay. In reverse beta-decay, electrons forced so close to a pole
of the proton, that through a w-particle, turn a proton into a neutron. Continued pressure eventully causes "layers" of proton
and neutrons shells to bind and become Helium, releasing enormous energy.
Falling deeper into the sun, the density rises eventually to 1.6×10^5 kg/m³. The movement of protons and electrons
are so severely restricted that electrons bind with protons forming neutrons. This process is a reverse
beta-decay. In reverse beta-decay, electrons forced so close to a pole
of the proton, that through a w-particle, turn a proton into a neutron. Continued pressure eventully causes "layers" of proton
and neutrons shells to bind and become Helium, releasing enormous energy.